Recurrences

This note is part of my learning notes on Data Structures & Algorithms.

---

Recurrence

A recurrence is an equation that describes the running time of a recursive algorithm. The general form of a recurrence relation is:

$$a_n = f(a_{n-1},a_{n-2}, ..., a_{n-k})$$

For example, the running time of the merge sort algorithm can be described by the recurrence $T(n) = 2T\frac{n}{2} + O(n)$, where $T(n)$ is the running time of the algorithm on an input size of $n$. We can solve this recurrence to find the running time of the algorithm for any input size.

More Examples

• Arithmetic Sequence

$$a_n = a_{n-1} + d$$

• Geometric Sequence

$$a_n = r \cdot a_{n-1}$$

• Fibonacci Sequence

$$F_n = F_{n-1} + F_{n-2}$$

Methods use to solve recurrences:

• Substitution Method
• Recursion Tree Method
• Master Theorem

---

Substitution Method

Substitution method solves recurrences by guessing the form of the solution and using mathematical induction to prove it.

Steps:

1. Based on the recurrence relation, make an educated guess about the asymptotic form of the solution. This guess is often based on experience or patterns observed in simpler cases.
2. Induction hypothesis: assume that the guessed form is correct for smaller values of $k$.
3. Inductive step: Prove that if the guess is correct for smaller values, it also holds for the general case $n$.
4. Verify that the solution holds for the initial conditions or base case.

---

Recursion Tree

Visualize the recurrence as a tree and sum the costs at each level.

Example: constructing a recursion tree for the recurrence $T(n) = 2T(\frac{n}{2}) + cn$

---

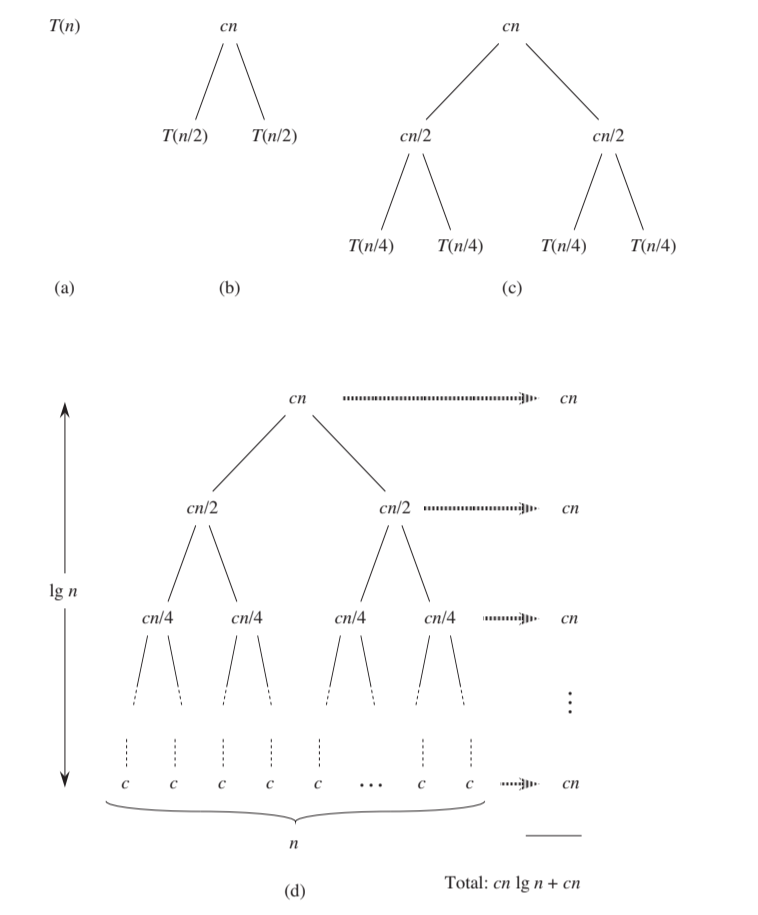
Master Theorem

The master theorem is a general method for solving recurrences of the form

$$T(n) = aT (\frac{n}{b}) + f(n)$$

where $a \geq 1$ and $b >1$

• $n$ : the size of the current problem
• $a$ : the number of subproblems in the recursion
• $\frac{n}{b}$ : the size of each subproblem
• $f(n)$ : the cost of the work that has to be done outside the recursive calls (cost of dividing + merging)

The Master Theorem gives asymptotic bounds for the solution to such recurrences by comparing $f(n)$ with $n^{log_b a}$:

• Case 1: Running time is dominated by the cost at the leaves
  • If $f(n) = O(n^{log_b a-\epsilon})$ for some $\epsilon > 0$, then

$$T(n) = \theta(n^{log_b a})$$

• Case 2: Running time is evenly distributed throughout the recursion tree
  • If $f(n) = \theta(n^{log_b a })$

$$T(n) = \theta(n^{log_b a} log(n))$$

• Case 3: Running time is dominated by the cost at the root
  • If $f(n) = \Omega(n^{log_b a + \epsilon})$

$$T(n) = \theta (f(n))$$

Steps

1. Extract $a$, $b$ and $f(n)$ from a given recurrence.
2. Determine $n^{log_b a}$
3. Compare $f(n)$ and $n^{log_b a}$
4. Determine which case to apply

---

Akra-Bazzi Theorem

The Akra-Bazzi theorem is a generalization of the master theorem that applies to recurrences of the form:

$$T(n) = \sum a_i T(b_i n) + f(n)$$

Steps

1. Extract $a_i, b_i$ and $f(n)$ from a given recurrence.

2. Find $\rho$, where $\rho$ is a unique real number such that $\sum^k_{i=1} a_i b_i^{\rho} =1$ (such $\rho$ always exist).

3. The solution for the recurrence is then

$$T(n) = \theta (n^{\rho} (1 + \int^n_1 \frac{g(u)}{u^{p+1}} du))$$

---

References

• John Bowers: Solved Recurrence Tree Method
• John Bowers: Solved Recurrence - Iterative Substitution