This note is part of my learning notes on Data Structures & Algorithms.

Linear Programming

Linear programming is an optimization technique for a system of linear constraints and a linear objective function. An objective function defines the quantity to be optimized, and the goal of linear programming is to find the values of the variables that maximize or minimize the objective function.

Formal Definition

Given:

  • nn number of Real-value variables

∀x⃗∈Rn\forall \vec{x} \in R^n

x⃗=(x1,x2,...,xn)\vec{x} = (x_1,x_2,...,x_n)

  • Linear objective function

c⃗⋅x⃗\vec{c} \cdot \vec{x}

  • mm number of Linear inequalities (constraints)

Ax≤bAx \leq b

AA is an n×dn \times d matrix

Goal: Find values for all xix_i that satisfy the constraints and maximize / minimize the objective function.

Simple Example of a LP problem

Given a max (objective function) 5x1+x25x_1 + x_2 , subjected to (s.t.) constraints:

{x1+x2≤7−2x1+3x2≥−4x1≥0,x2≥0\begin{cases} x_1 + x_2 \leq 7 \\ -2x_1 + 3x_2 \geq -4 \\ x_1 \geq 0, x_2 \geq 0 \\ \end{cases}

Find the values of x1x_1 and x2x_2, so that 5x1+x25x_1 + x_2 has a max value.

Simplex Method

Simplex method is an algorithm used to solve linear programming problems.

Given the objective function and inequality constraints,

maxxx4max_{x} x_4 \\

s.t {x1=0x2−x1≤1x3−x2≤3x3−x1≤6x4−x3≤1x4−x2≤5\text{s.t } \begin{cases} x_1 = 0 \\ x_2 - x_1 \leq 1 \\ x_3 - x_2 \leq 3 \\ x_3 - x_1 \leq 6 \\ x_4 - x_3 \leq 1 \\ x_4 - x_2 \leq 5 \\ \end{cases}

  1. Convert the inequalities into equations by adding one slack variable for each inequality

{x4=0x1+y1=0x2−x1+y2=1x3−x2+y3=3x3−x1+y4=6x4−x3+y5=1x4−x2+y6=5\begin{cases} x_4 = 0 \\ x_1 + y_1 = 0 \\ x_2 - x_1 + y_2 = 1 \\ x_3 - x_2 + y_3 = 3 \\ x_3 - x_1 + y_4 = 6 \\ x_4 - x_3 + y_5 = 1 \\ x_4 - x_2 + y_6 = 5 \\ \end{cases}

  1. Construct the initial simplex tableau

  2. The most negative entry in the bottom row identifies the pivot column.

     https://math.libretexts.org/Bookshelves/Applied_Mathematics/Applied_Finite_Mathematics_(Sekhon_and_Bloom)/04%3A_Linear_Programming_The_Simplex_Method/4.02%3A_Maximization_By_The_Simplex_Method

Now we’ll use linear programming to model some algorithm problems.

Example: Max-Flow

Find the max flow in G(V,E)G(V,E) from source node ss to sink node tt.

max∑v:(s,v)∈Ef(s,v)s.t∑u:(u,v)∈Ef(u,v)=∑w:(v,w)∈Ef(v,w),∀v∈V−{s,t}\begin{aligned} & max \sum_{v:(s,v)\in E} f(s,v) \\ &s.t \sum_{u:(u,v) \in E} f(u,v) \\ &= \sum_{w:(v,w) \in E} f(v,w) , \forall v \in V - \{s,t\} \end{aligned}

Capacity constraint:

0≤f(u,v)≤c(u,v),∀(u,v)∈E0 \leq f(u,v) \leq c(u,v), \forall(u,v) \in E

Because the capacity constraints and flow conservation rule of the flow network can be used as the constraints for linear programming. Hence, we model it with linear programming.

Example: Min-Cost Max Flow

  1. Ignore cost, get max flow ff

min∑(u,v)∈E\begin{aligned} min \sum_{(u,v) \in E} \end{aligned}

Example: L1 Regression

Given a set of points (x1,y1)(x2,y2)...(xn,yn)(x_1, y_1)(x_2,y_2)...(x_n,y_n) want to fit a line (hyperplane) such that the vertical distance between the predicted value of yy and that actual value is small, summed over all the points.

Suppose we predict y=ax+by=ax+ b , the error for point (xi,yi)=(axi+b)−yi(x_i,y_i) = (ax_i +b )-y_i

To solve L1 Regression, we turn it into a Linear Programming problem.

Turn the constraints into

subject to{axi+b−yi≤ziaxi+b−yi≥zi\text{subject to} \begin{cases} ax_i + b - y_i \leq z_i \\ ax_i + b - y_i \geq z_i \end{cases}

The objective function is

min∑izimin \sum_{i} z_i

Example: Compressing Sensing

Constructing A∈Rk×dA \in \\R^{k \times d}

k=Ω(slogDS), (k<<D)k = \Omega (s log \frac{D}{S}) , \text{ } (k << D)

whose entries are independently taken from an independent Normal distribution Normal(0,1)Normal(0,1).

The objective function is

min∣x⃗∣=min∑izi\begin{aligned} &min | \vec{x} | \\ &= min \sum_{i} z_i \end{aligned}

The constraints are

s.t. Ax⃗=b⃗−zi≤xi≤zizi≥0\begin{aligned} &\text{s.t. } A\vec{x} = \vec{b} \\ & -z_i \leq x_i \leq z_i \\ & z_i \geq 0 \end{aligned}

Standard Form

Standard form is the starting point for using the simplex method to solve linear programming problems.

We say that a linear programming problem is in standard form if the following are all true:

  1. Non-negativity constraints for all variables (RHS value of inequality is non-negative)
  2. All remaining constraints are expressed as equality constraints
  3. The right hand size b⃗\vec{b}is non-negative

max (c⃗)T⋅x⃗\text{max } (\vec{c})^T \cdot \vec{x}

s.t. {Ax⃗≤b⃗x≥0\text{s.t. } \begin{cases} A \vec{x} \leq \vec{b} \\ x \geq 0 \end{cases}

Below are some tricks to change non-standard form linear programming problems into standard form. Changing them into standard form makes it easier to solve duality.

Trick 1: Inequality the wrong way

5x1−3x2≤7−5x1+3x2≥−7\begin{aligned} 5x_1 - 3x_2 \leq 7 \\ -5x_1 + 3x_2 \geq -7 \end{aligned}

Trick 2: Equality

Trick 3: xix_i unbounded

Trick 4: Max = Min 1t\frac{1}{t} or Max = Min −t-t

Converting min to max Suppose we have a minimization LP. Then we can negate the objective function and make it a maximization problem instead.

Example: Find Shortest Path

Each edge e=(u,v)e=(u,v) has weights w(u,v)w(u,v), in which the weights can be positive or negative.

Assuming there’s no cycle

1st Attempt: Min-Cost Flow

We send a 1-unit flow from the source node ss to sink node tt . It can go through any edge, we want to find the min-cost for it.

min∑(u,v)∈Ew(u,v)⋅f(u,v)min \sum_{(u,v) \in E} w(u,v) \cdot f(u,v)

s.t.{∑(s,u)∈Ef(s,u)=1∑u:(u,v)∈Ef(u,v)=∑w:(v,w)∈Ef(v,w),∀v∈V−{s,t}f(u,v)≥0\text{s.t.} \begin{cases} \sum_{(s,u) \in E} f(s,u) = 1 \\ \sum_{u:(u,v) \in E} f(u,v) = \sum_{w:(v,w) \in E} f(v,w), \forall v \in V-\{s,t\} \\ f(u,v) \geq 0 \end{cases}

Claim: The flow will only be on the shortest path from ss to tt .

2nd Attempt: Max Distance

max d(t)\text{max } d(t)

s.t. {d(v)≤d(u)+w(u,v),∀(u,v)∈Ed(s)=0\text{s.t. } \begin{cases} d(v) \leq d(u) + w(u,v), \forall (u,v) \in E \\ d(s) =0 \end{cases}

The 1st and 2nd attempt aim to solve the problem in different ways but lead to same solutions. They are dualities.

Primal and Dual LP

https://www.reisanar.com/files/Primal_Dual.pdf

Formal Definition

(I) and (II) are dualities.

(I) For every primal LP problem in the form of

maximize (c⃗)T⋅x⃗\text{maximize } (\vec{c})^T \cdot \vec{x}

s.t. {Ax⃗≤b⃗x⃗≥0⃗\text{s.t. } \begin{cases} A\vec{x} \leq \vec{b} \\ \vec{x} \geq \vec{0 } \end{cases}

(II) There exists an equivalent dual LP problem

minimize b⃗⋅y⃗\text{minimize } \vec{b} \cdot \vec{y}

s.t. {ATy⃗≥c⃗y⃗≥0⃗\text{s.t. } \begin{cases} A^T\vec{y} \geq \vec{c} \\ \vec{y} \geq \vec{0 } \end{cases}

Constructing a dual LP from a primal LP

Given a primal LP

max z=2x1−x2\text{max }z = 2x_1 - x_2

s.t. {x1−x2≤1−x1+x2≤−2x1≥0,x2≥0\text{s.t. } \begin{cases} x_1 - x_2 \leq 1 \\ -x_1 + x_2 \leq -2 \\ x_1 \geq 0, x_2 \geq 0 \end{cases}

  1. Convert into standard form

max (c⃗)T⋅x⃗\text{max } (\vec{c})^T \cdot \vec{x}

s.t. {Ax⃗≤b⃗x⃗≥0⃗\text{s.t. } \begin{cases} A\vec{x} \leq \vec{b} \\ \vec{x} \geq \vec{0 } \end{cases}

where:

(c⃗)T=(2−1)(\vec{c})^T = \begin{pmatrix} 2 \\ -1 \end{pmatrix}

A=(1−1−11)A = \begin{pmatrix} 1 & -1 \\ -1 & 1 \end{pmatrix}

b⃗=(1−2)\vec{b} = \begin{pmatrix} 1 \\ -2 \end{pmatrix}

  1. Objective Function: The coefficients of b⃗ \vec{b} \text{ }in the primal become the objective coefficients in the dual. (Because maximizing in the primal = minimizing in the dual)

  2. Constraints: The coefficients of the primal constraints AA become the transpose of AA in the dual constraints.

  3. Right-Hand Side: The coefficients of the primal objective function cc become the right-hand side constants in the dual constraints.

  4. Non-negativity: The variables corresponding to the primal constraints (dual variables) must be non-negative.

  5. Hence the dual LP is:

min w=y1−2y2\text{min } w = y_1 - 2y_2

s.t. {y1−y2≥2−y1+y2≥−1y1≥0,y2≥0\text{s.t. } \begin{cases} y_1 - y_2 \geq 2 \\ -y_1 + y_2 \geq -1 \\ y_1 \geq 0, y_2 \geq 0 \\ \end{cases}

Weak Duality Theorem

If x⃗\vec{x}is a feasible solution to the Primal LP, and y⃗\vec{y} i a feasible solution to the Dual.
Then

(c⃗)Tx⃗≤(y⃗)Tb(\vec{c})^T \vec{x} \leq (\vec{y})^T b

Strong Duality Theorem

Suppose the Primal LP is feasible and bounded (not infinitely large), then the Dual LP’s solution is also feasible and bounded. Moreover, their optimal solution x∗⃗\vec{x*}and y∗⃗\vec{y*} satisfies

(c⃗)Tx⃗=(y⃗)Tb(\vec{c})^T \vec{x} = (\vec{y})^T b

max of primal = min of dual

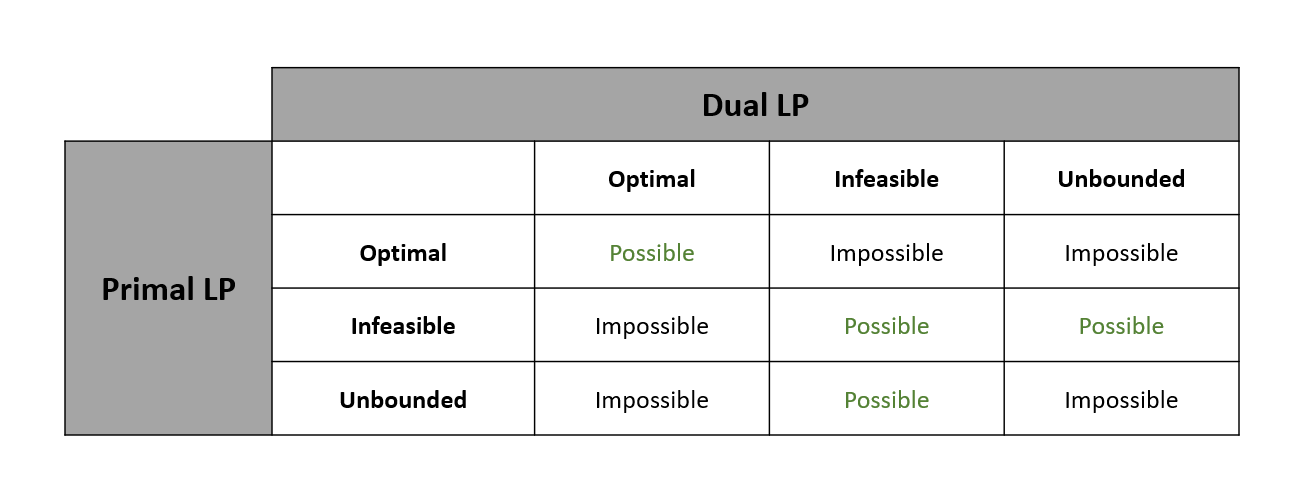
Using Duality to Determine Feasibility & Boundedness of LP

  • Infeasible: there is no point that satisfies the constraints
  • Feasible & Bounded (Optimal): there is a feasible point of maximum objective function value
  • Feasible & Unbounded: there are feasible points of arbitrarily large value

Example: 2-Player Zero Sum Game

References