Hash Tables

This note is part of my learning notes on Data Structures & Algorithms.

---

Introduction

Hash tables are a type of data structure that allows fast INSERT/DELETE/SEARCH operations. Each operation will take constant time $O(1)$.

• Insert(k): Insert key $k$ into the hash table.
• Lookup(k): Check if key $k$ is present in the table.
• Delete(k): Delete the key $k$ from the table.

Let $U$ be the universe of all keys, the size of this universe is $M$, where $M$ is really big. In a hash table of size $n$, each key $k \in U$ is mapped to one of $n$ “buckets” by a hash function.

A hash function $h: U \rightarrow \{ 1,...,n\}$ is a mathematical function that takes an input and returns an output of fixed-size string of bytes, which is typically a hash value (maps elements of $U$ to buckets $1,...,n$). This value is often represented as a hexadecimal number.

Examples of hash function:

• division
• multiplication
• universal hashing
• dynamic perfect hashing
• static perfect hashing

This technique called hashing determines an index or location for the storage of an item in a data structure.

---

Random Hash Functions

We want a hash table to not have too many buckets (to save space), and we want the items to be spread-out in the buckets (enable fast operations). Hence, we incorporate randomness in hashing. There are two ways to do so:

1. Assume that the set of keys stored in the hash table is random, or
2. Assume that the hash function $h$ is random.

Let there be $n$ number of keys, $X$ be the size of the hash bucket that $x_i$ maps to. The expected cost of performing any of the operations INSERT/DELETE/SEARCH with a random hash function is:

$$\begin{aligned} E[X] &= \sum^{n}_{j=1} Pr\left[ h(x_i) = h(x_j) \right] \\ &= 1 + \sum^{n}_{j \neq i} Pr\left[ h(x_i) = h(x_j) \right] \\ &= 1 + \frac{n-1}{n} \\ &\leq 2 \end{aligned}$$

When $h$ is random,

$$Pr\left[ h(x_i) = h(x_j) \right] = \frac{1}{n}$$

Algorithm:

1. Choose any $n$ items $u_1, u_2, ..., u_n \in U$, and any sequence of INSERT/DELETE/SEARCH operations on these items.
2. Choose a random hash function $h: U \rightarrow \{ 1,...,n\}$.
3. Hash it out.

---

Collisions

Suppose there’s an array $A$ of some size $M$ and a hash function $h: U \rightarrow \{0,...,M-1\}$. A collision is when $h(x) = h(j)$ for two different keys $x$ and $y$.

Claim: for any hash function $h$, if $|U| \geq (N-1)M+1$, there exists a set $S$ of $N$ elements that all hash to the same location.

We can handle collision with a method called separate chaining, by having each entry in $A$ be a linked list. To insert an element, we just put it at the top of the list. If $h$ is a good function, then we hope that the lists will be small.

---

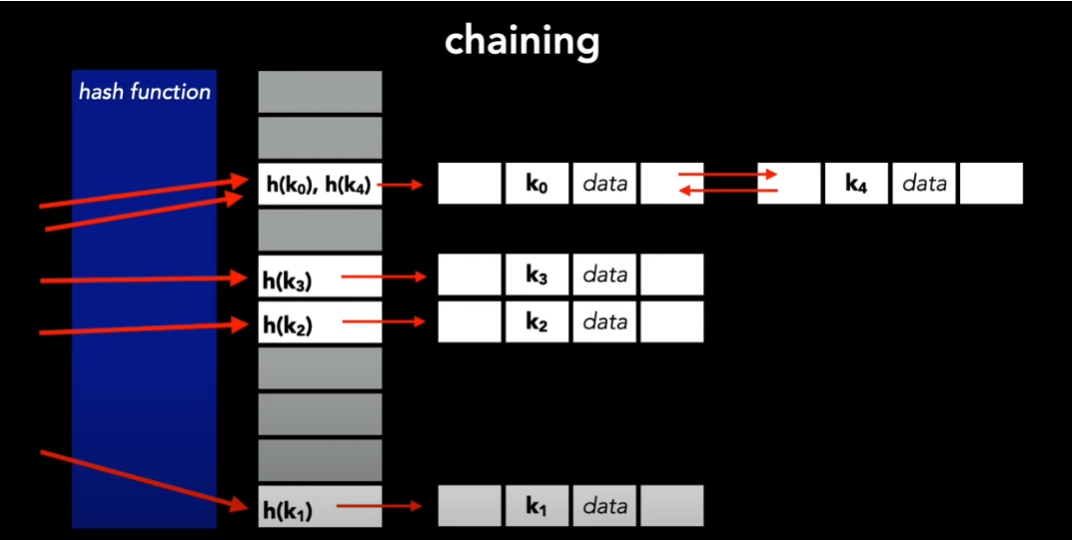
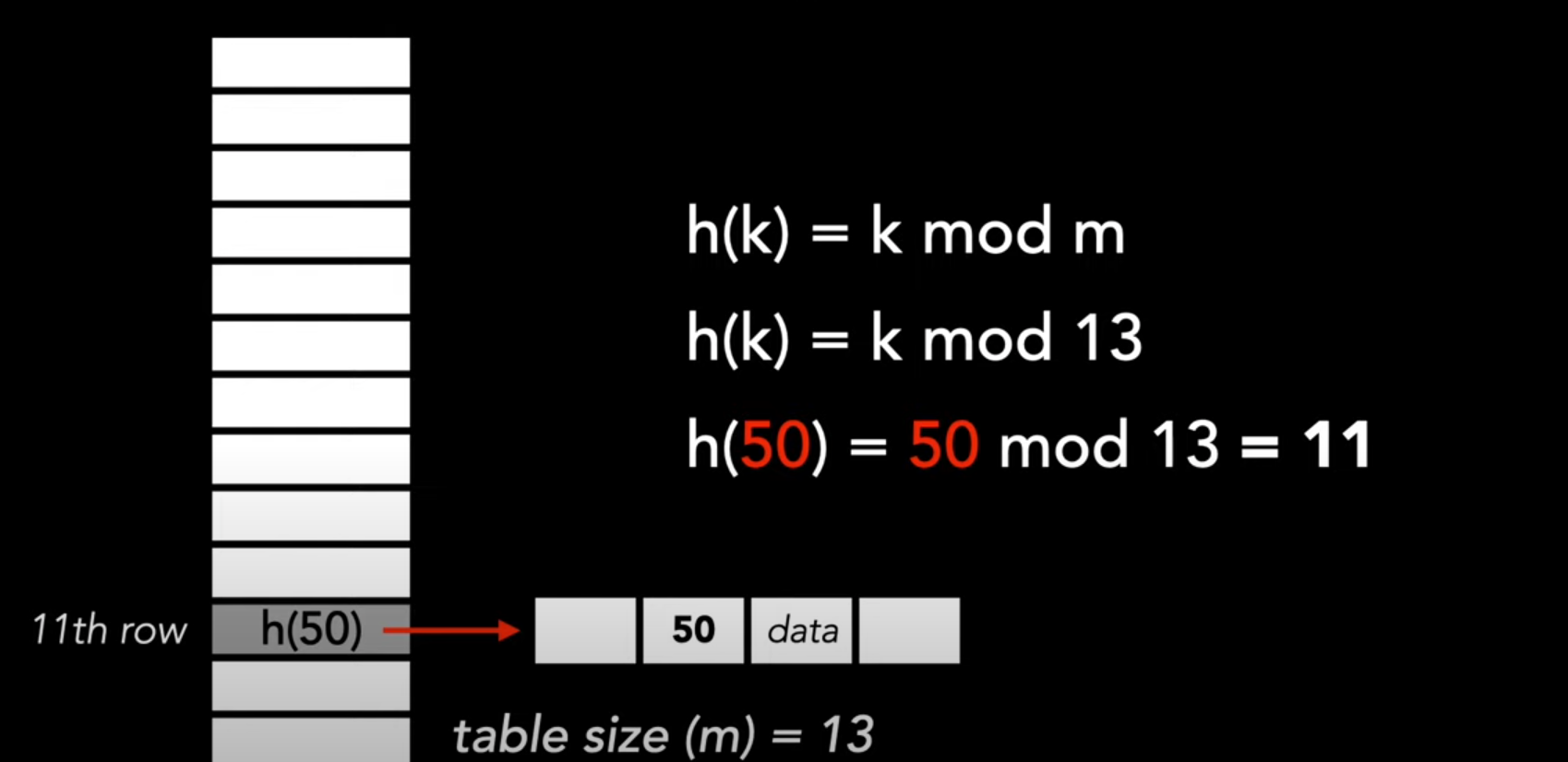
Hashing By Division

Suppose there is a hash table of size $m$, using division, the hash function is:

$$h(k) = k \text{ } mod \text{ } m$$

---

Universal Hashing

A uniformly random hash function can lead to balanced buckets, decreasing the number of collisions, and ensuring all INSERT/DELETE/SEARCH operations take $O(1)$ constant time. But it’s not a good idea to use this method because we will have to store them and there’s $n^M$ of them. Writing down a random one of them takes $log(n^m)$ bits, which is $M log(n)$.

The solution is to pick from a smaller set of hash functions. This chosen subset collection of hash functions is called a hash family $H$. When $h$ is chosen uniformly at random from $H$, it is said to be universal if: for each pair of different keys $x$ and $y \in U$, the the probability that they hash to the same value (collision) is at most $\frac{1}{m}$.

Formally: $H$ is universal if:

$$\forall x,y \in U, x \neq y$$

$$Pr\left[ h(x) = h(y) \right] \leq \frac{1}{m}$$

For a small universal hash family of size $O(m^2)$, we need only $O(log \text{ }m)$ bits to store it.

Properties of Universal Hashing

1. Low Collision Probability: Universal hashing ensures that the probability of any two distinct keys colliding is low, specifically at most $\frac{1}{m}$.
2. Uniform Distribution: When a hash function is chosen randomly from a universal family, the hash values are uniformly distributed over the range, reducing the chances of clustering.
3. Independence: The choice of hash function is independent of the keys, making it less likely for an adversary to predict collisions.
4. Efficiency: Universal hash functions can be computed efficiently, typically in constant time $O(1)$.

Theorem

For $n$ arbitrary distinct keys, and for random hash function chosen from universal hash family $h \in H$

$$\begin{aligned} E(num \text{ } of \text{ } keys \text{ } in \text{ } slot \text{ } that \text{ } collide) &\leq 1 + \alpha \\ &\leq 1+ \frac{n}{m} \end{aligned}$$

Matrix method

The matrix method is a way to construct a universal hash family.

---

Perfect Hashing

Perfect hashing is a type of hashing that guarantees no collisions for a given set of keys, providing optimal performance with $O(1)$ lookup time.

We say a hash function is perfect for a set $S \in U$ if it maps all elements of $S$ to distinct values

$$h: S \rightarrow \{0,1,...,m-1\}$$

such that

$$\forall x,y \in S, x \neq y$$

$$h(x) \neq h(y)$$

Types of Perfect Hashing

• Static Perfect Hashing: A perfect hash function where a set of keys is fixed, and the function ensures no collisions among these keys.
• Dynamic Perfect Hashing: A perfect hash function that can handle a changing set of keys without collisions.

Properties of Perfect Hashing

• No collisions: by definition, a perfect hash function guarantees no collisions among the keys in the set $S$
• Efficiency: optimal performance with $O(1)$ lookup time.

---

Example: Balls And Bins Model

The balls and bins model is a probabilistic model used to analyze random allocation or distribution of objects. In this model, a set of balls represent distinct objects, and a set of bins represent distinct containers or possibilities.

I. No Collision (Birthday Paradox)

Suppose we throw $n$ balls randomly into $m$ bins. (Here the balls represents the keys to be hashed and the bins represent the slots in the hash table)

Probability that no two balls collide:

$$\begin{aligned} Pr\left[ no \text{ } 2 \text{ } balls \text{ } collide \right] &= 1 \times \left( \frac{m-1}{m}\right) \times \left( \frac{m-2}{m}\right) \times ... \times \left( \frac{m-n+1}{m}\right) \\ &= \frac{(m-1)(m-2)...(m-n+1)}{m^{n-1}} \\ &= 1 - \left( \frac{1}{m} \right)^{n-1} \end{aligned}$$

This shows us how large $m$ needs to be to have no collisions.

Max Load

Suppose $m=n$, which means we throw $n$ balls randomly into $n$ bins. What is the maximum number of balls in any bin?

---

Example: Bloom Filter

A Bloom filter is a space-efficient, probabilistic data structure that is based on hashing. It is typically used to add a hash of the elements to a set to determine whether that element belongs to a set. Example: checking the availability of a username.

A Bloom filter is similar to a hash table, where it will use a hash function to map a key to a bucket. However, it will not store that key directly in that bucket, instead it will hash it into multiple hash functions and simply mark the bucket as filled. Hence some keys might map to the same filled bucket, causing false positives.

False positives occur when an element is not present in the original set, but the Bloom filter mistakenly indicates that it is. The probability of a false positive $Pr(FP)$ depends on the number of elements inserted into the filter $n$ and the capacity of the filter $M$

$$Pr(FP) = (1 - e^{-\frac{m}{h}})^h$$

Steps to using a Bloom filter:

1. Get input
2. Calculate hash value
3. Mod the hash
4. Insert the hash
5. Lookup the value

---

Conclusion

A hash table can be designed such that it

• has hash function that maximizes randomness and produce least amount of collisions
• supports INSERT/DELETE/SEARCH operations in $O(1)$ expected time
• requires $O(nlog(M))$ bits of space.
  • $O(n)$ buckets
  • $O(n)$ items with $log(M)$ bits per item
  • $O(log(M))$ to store the hash function

U: universe
u: number of possible keys in universe
n: number of actual keys to store in hash table
k: key
x,y: a pair of distinct keys
m: size of hash table / number of slots in table / number of buckets

---

References

• Stanford CS161: Hashing
• CMU 15-451: Universal and Perfect Hashing
• [Brilliant: Bloom Filter](https://brilliant.org/wiki Bloom-filter/)
• [Geeksforgeeks: Bloom Filter](https://www.geeksforgeeks.org Bloom-filters-introduction-and-python-implementation/)
• Duke University CPS102: Probability in hashing